Vectors

Vector is a quantity having Direction as well as Magnitude

Vectors

Just like the image above :

Side 1 which is a and Side 2 which is b. If you want to find the Side 3 which is c.

You use the equation a² + b² = c² (Note : This is for Right Triangle)

Example :

a = 3 b = 4 so c = 3² + 4² = 5²

If the triangle is not a Right Triangle use this equation instead :

R =  √((F₁² + F₂²) + 2 * F₁ * F₂ * Cos  Θ)

Example : 

F₁ = 3 F₂ = 4 and Θ = 60

R = √((3² + 4²) + 2 * 3 * 4 * Cos (60))

R = √(25 + 2 * 3 * 2) = √(25 + 12) = √37 which is  ≈ 6.08

Just like the image above :

Side 1 = Side 3 which is a and Side 2 = Side 4 which is b. If you want to find the Side 5 which is c.

You use the equation a + b / b + a = c (Note : This is for parallelogram)

Example ;

a = 3 and b = 1 so c = 3 + 1 = 4

R_min ≤ R ≤ R_max While R_min = F₁ - F₂ and R_max = F₁ + F₂

Now using this Triangle we have this equation :

Sin = y ÷ r and Cos = x ÷ r while Tan = y ÷ x

From this we know that F_x = F * Cos Θ  and F_y = F * Sin Θ

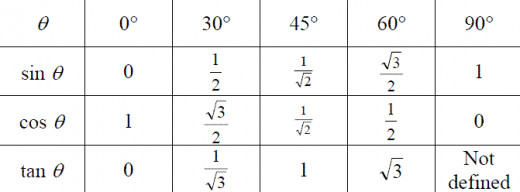
Now to find the Magnitude and Direction of the vectors use this equation :

Magnitude = √ΣF_x² + ΣF_y²

Direction = Tan Θ = ΣF_y ÷ ΣF_x

Example :

F₁ = 5 N with Θ = 30

F₂ = 3 N with Θ = 60

F_1y = 5 Cos(30) ≈ 4.33

F_1x = 5 Sin(30) = 2.5

F_2y = 3 Cos(60) = 1.5

F_2x = 3 Sin(60) ≈ 2.60

Magnitude = √4² + 6.9² ≈ 8

Direction = 6.9 ÷ 4 = 1.725

Dot and Cross Product

Dot Product also called Scalar Product. Geometrically the Dot Product of 2 vectors is Magnitude of one time projection of the second onto the first.

A . B = (A_xI + A_yJ + A_zK) . (B_xI + B_yJ + B_zK)

A . B = A_xB_x + A_yB_y + A_zB_z

Same Angle

I . I = J .J = K . K = (1) (1) (Cos 0) = 1

Different Angle

I . J = J . K = K . I = (1) (1) (Cos 90) = 0

Example :

A = 8m

B = 10m

A . B = A B Cos 37 = 8 10 0.8 = 64m

Cross Product also called Vector Product. Geometrically the Cross Product of 2 vectors is area of parallelogram between them.

A x B = C

A is the first, B is the second and C is the resultant. There is a right hand rule to determine the direction of the resultant. Just imagine that A is your finger, B is palm and C is your thumb.

Example :

If A is going to North and B is going to West. Just point your finger to North and face your palm to the West and see where is your thumb pointing at. Your thumb should be pointing Upwards.

I x I = J x J = K x K = (1) (1) (Sin 0) = 0

         I

K               J  

Now this is the IJK Triangle. If it turns in clockwise the result is positive but if it turns in anti-clockwise the result is negative.

Example ;

A = 4i + 3j - 2k

B = 7i + 2j + 5k

A x B = 8k - 21k - 13k - 14j - 20j - 34j + 15i + 4i + 19i = 38i - 68j - 26k

Measurements

Measuring is a process of the object in SI Unit.

Uncertainty

Uncertainty is the uncertain of the Measurement.

To find the Uncertainty in Vernier Caliper and Micrometer use this Formula :

▲X = ½ * Smallest Scale

Examples :

Vernier Caliper's Smallest Scale is 0.1 thus ▲X = ½ * 0.1 = 0.05 mm

Micrometer's Smallest Scale is 0.01 thus ▲X = ½ * 0.01 = 0.005 mm

Vernier Caliper

Look at the Picture. To read its Measurement first look at the Measurement of the First Scale. It stops at 10 cm. Then look at the Second Scale find the scale which is Aligned. Its 2 so its 0.2 cm.
Then sum it up 10.2 cm ± (Uncertainty) Which is 0.05 mm

Micrometer

Look at the Picture. To read its Measurement first look at the Measurement of the First Scale. It stops at 2.5 mm. Then look at the Second Scale fine the scale which is Aligned at the Picture. Its 12 so its 0.12 mm.

Then sum it up 2.62 mm ± (Uncertainty) Which is 0.005 mm

Another way to find Uncertainty is using this Formula :

1 ÷ N √((N(ΣI²) - (ΣI)²) ÷ (N - 1))

Example : (All in kg)

N                   I                   I²

1                   1                  1

2                   2                  4

3                   3                  9

4                   4                  16

5                   5                  25

1 ÷ 5 * √((5(55) - (15)²) ÷ (5 - 1)) = 1 ÷ 5 * √((275 - 225) ÷ 4) = 1 ÷ 5 * √(50 ÷ 4)

= 1 ÷ 5 * √12.5 ≈ 1 ÷ 5 * 3.54 ≈ 0.88 kg

Then find the Average of ΣI which is 15 ÷ 5 = 3 kg

Then the report of  the measurement is 3 kg ± 0.88 kg

To find the Accuracy use this Formula :

Uncertainty ÷ Average of ΣI * 100

Example :

0.88 ÷ 3 * 100 = 29%

Dimension

Dimension is an expression of the character of a derived quantity in relation to fundamental quantities, without regard for its numerical value.

Base Quantity                                         Dimension

Length                                                           L

Mass                                                             M

Time                                                              T

Current                                                          I

Temperature                                                 Θ (tetha)

Light Intensity                                               J

Number of Substance                                   N

Examples :

Normal Gravity is Meter / Second² so its [L] [T]^-2

Force is Mass * Meter / Second² so its [M] [L] [T]^-2

Work is Mass * Meter / Second² * Length so its [M] [L]² [T]^-2

Power is Mass * Meter / Second² * Length ÷ Second so its [M] [L]² [T]^-3

Sound Intensity is (Mass * Meter / Second² * Length ÷ Second) ÷ Meter² so its [M] [T]^-3