Projectile and Circular Motion

Projectile Motion

Projectile motion is a form of motion in which an object or particle (called a projectile) is thrown near the earth's surface, and it moves along a curved path under the action of gravity only. The only force of significance that acts on the object is gravity, which acts downward to cause a downward acceleration.

To find Vo_y , Vo_x and time use this equation : (Y₀ is initial height)

Vo_y = Vo * Sin Θ                Vo_x = Vo * Cos Θ                0 = Y₀ + Vo_y * t + 0.5 * g * t²

To find the Magnitude of projectile motion use this equation :

Vo = √(Vo_y² + Vo_x²)

To find the Direction of projectile motion use this equation :

Tan Θ = Vo_y ÷ Vo_x

To find the max range of projectile motion use this equation :

X = Vo_x * time

To find the max height of projectile motion use this equation :

X_H =  Vo_y² / 2g


Examples : 

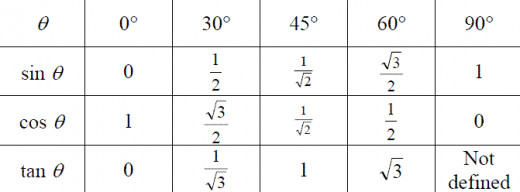
if Vo = 10 and Θ = 30 then first we must find the time by using Vo_y / g which is 10 * Sin 30 = 5 / 10, but it is only the time to reach the max height thus 0.5 * 2 is the time for max range which is 1 second.
Now to find the max range get the Vo_x by 10 * Cos 30 = 5√3 and times it with the time which is 1 second so the max range is 5√3

Circular Motion

Circular Motion is a movement of object along side of the circumference of a circle or rotation along a circular path.

In Circular Motion V is changed to Ω which is omega while a = α which is alpha.

Equation used in Circular Motion :

V = Ω * R (R is radius) this is used to describe relation between angular velocity and linear velocity

a = α * R (in rad/s²) this is used to describe relation between angular accel and linear accel

V_1 = V₀ + a * t (in m/s)

Ω_{1  =} Ω₀ + α * t (in rad/s)

a_c = V² / R (in rad/s²)

α_c = Ω² / R (in rad/s²)

F_c = M * α_c (in newton) this is used to find centripetal force

V = √(µ_s * g * R) (µ_s dry = 0.9 ice = 0.1) this is used to find velocity needed to turn on cliff

V = √((G * M_earth) / R) this is used to find velocity of satellites revolving the earth


Converting cycle = ° = rad

1 cycle = 360° = 2π rad

Examples : 

Convert to radian : 
180° = 180 / 360 * 2π rad = π rad
90° = 90 / 360 * 2π rad = π / 2 rad

Convert to ° :
π / 4 rad = (π / 4) / 2π * 360 = 45°
3π / 4 rad = (3π / 4) / 2π * 360 = 135°


Circular Motion in 2 Wheels

For the first picture V₁ = V₂ while the second picture  Ω₁ = Ω₂ 

Examples : 

The first picture if R1 = 10, R2 = 20 and  Ω₁ = 1 then ? = Ω₂

To solve this use the equation V = Ω * R. First find the V which is 1 * 10 = 10, then using the same equation 10 = Ω₂ * 20 which is 10 / 20 = 0.5 rad/s

The second picture if R1 = 10, R2 = 20 and V₁ = 10 then ? = V₂ 

To solve this use the equation V = Ω * R. First find the Ω which is 10 / 10 = 1, then using the same equation V₂ = 1 * 20 which is 20 m/s 

Linear Motion

Quantities

There are several Quantities in Linear Motion

• Distance
• Displacement
• Speed
• Velocity
• Acceleration
• Average value of Velocity and Acceleration
• Instantaneous value of Velocity and Acceleration
• *Vertical Motion*

Equation

There is 3 Equation in Linear Motion

The First one provides the relation between Initial Velocity, Final Velocity, The Time taken to reach it and The Acceleration.

The Second one provides the relation between Distance Traveled, Initial Velocity, Acceleration and Time.

The Third one provides the relation between Initial Velocity, Final Velocity, Acceleration and Distance. There is no time factor in it.

So the Equation is written as:

1st Acceleration = (Final Velocity - Initial Velocity) / Time or Final Velocity = Initial Velocity + Acceleration * Time

2nd Distance/Displacement = Initial Velocity * Time + (Acceleration * Time²) / 2

3rd Final Velocity² = Initial Velocity² + 2 Acceleration * Distance/Displacement

If it is used for a free fall object change all Acceleration to Gravity.

Examples :

1. A ball was released from a building and after 5 seconds it reached the ground. What is the maximum velocity of the ball?

Since it is a free fall the acceleration is 10 m/s² so in equation its 10 = (Final Velocity - 0) / 5

10 * 5 = Final Velocity , so the maximum velocity of the ball is 50 m/s.

2.  A ball was released from a building and after 5 seconds it reached the ground. What is the height of the building?

Since it is a free fall the acceleration is 10 m/s² and the Initial Velocity is 0 m/s so in equation it is

S = 0 * 5 + 10 * 5² / 2

S = 0 + 250 / 2

S = 125 m

So the height of the building is 125 m

3. A plane that starts from rest then with a velocity of 100 m/s and acceleration of 2 m/s² is going to take off. Calculate the minimum distance that must be traveled before taking off.

Since its starting from rest so the Initial Velocity is 0 m/s so in equation it is

100² = 0² + 2 * 2 * S

10000 = 2 * 2 * S

S = 10000 / 4

S = 2500 m

So it needs to travel 2500 m before taking off.

Graph in Linear Motion

In Linear Motion there is two types of graphs, the first one is Position vs Time and the second one is Velocity vs Time.

Position vs Time

There is 2 types of Position vs Time graphs. It is Positive and Negative. If it is Positive it means that it is going forward while if it is Negative it means that it is going backward. 

The Equation is (Final Position - Initial Position) / (Final Time - Initial Time).

To find the result which is velocity, we divide the position with the time. So for this graph its velocity is

(10 - 0) / (5 - 0) = 2 m/s

(20 - 10) / (10 - 5) = 2 m/s

(30 - 20) / (15 - 10) = 2 m/s

So the velocity is 2 m/s going forward while if it is reversed 

(20 - 30) / (5 - 0) = -2 m/s

(10 - 20) / (10 - 5) = -2 m/s

(0 - 10) / (15 - 10) = -2 m/s

So the velocity is -2 m/s going backward it is written in minus but the + and - is just a sign whether it is going forward or backward.

Velocity vs Time

There is 2 types of Velocity vs Time graphs. It is Positive and Negative. If it is Positive it means that it is going forward while if it is Negative it means that it is going backward. 

The equation is (Final Velocity - Initial Velocity) / (Final Time - Initial Time).

To find the result which is acceleration, we divide the velocity with the time. So for this graph its acceleration is

(10 - 0) / (1 - 0) = 10 m/s²

(20 - 10) / (2 - 1) = 10 m/s²

(30 - 20) / (3 - 2) = 10 m/s²

(40 - 30) / (4 - 3) = 10 m/s²

(50 - 40) / (5 - 4) = 10 m/s²

So the acceleration is 10 m/s² going forward while if it is reversed

(40 - 50) / (1 - 0) = -10 m/s²

(30 - 40) / (2 - 1) = -10 m/s²

(20 - 30) / (3 - 2) = -10 m/s²

(10 - 20) / (4 - 3) = -10 m/s²

(0 - 10) / (5 - 4) = -10 m/s²

So the acceleration is -10 m/s² going backward it is written in minus but the + and - is just a sign whether it is going forward or backward.

Vectors

Vector is a quantity having Direction as well as Magnitude

Vectors

Just like the image above :

Side 1 which is a and Side 2 which is b. If you want to find the Side 3 which is c.

You use the equation a² + b² = c² (Note : This is for Right Triangle)

Example :

a = 3 b = 4 so c = 3² + 4² = 5²

If the triangle is not a Right Triangle use this equation instead :

R =  √((F₁² + F₂²) + 2 * F₁ * F₂ * Cos  Θ)

Example : 

F₁ = 3 F₂ = 4 and Θ = 60

R = √((3² + 4²) + 2 * 3 * 4 * Cos (60))

R = √(25 + 2 * 3 * 2) = √(25 + 12) = √37 which is  ≈ 6.08

Just like the image above :

Side 1 = Side 3 which is a and Side 2 = Side 4 which is b. If you want to find the Side 5 which is c.

You use the equation a + b / b + a = c (Note : This is for parallelogram)

Example ;

a = 3 and b = 1 so c = 3 + 1 = 4

R_min ≤ R ≤ R_max While R_min = F₁ - F₂ and R_max = F₁ + F₂

Now using this Triangle we have this equation :

Sin = y ÷ r and Cos = x ÷ r while Tan = y ÷ x

From this we know that F_x = F * Cos Θ  and F_y = F * Sin Θ

Now to find the Magnitude and Direction of the vectors use this equation :

Magnitude = √ΣF_x² + ΣF_y²

Direction = Tan Θ = ΣF_y ÷ ΣF_x

Example :

F₁ = 5 N with Θ = 30

F₂ = 3 N with Θ = 60

F_1y = 5 Cos(30) ≈ 4.33

F_1x = 5 Sin(30) = 2.5

F_2y = 3 Cos(60) = 1.5

F_2x = 3 Sin(60) ≈ 2.60

Magnitude = √4² + 6.9² ≈ 8

Direction = 6.9 ÷ 4 = 1.725

Dot and Cross Product

Dot Product also called Scalar Product. Geometrically the Dot Product of 2 vectors is Magnitude of one time projection of the second onto the first.

A . B = (A_xI + A_yJ + A_zK) . (B_xI + B_yJ + B_zK)

A . B = A_xB_x + A_yB_y + A_zB_z

Same Angle

I . I = J .J = K . K = (1) (1) (Cos 0) = 1

Different Angle

I . J = J . K = K . I = (1) (1) (Cos 90) = 0

Example :

A = 8m

B = 10m

A . B = A B Cos 37 = 8 10 0.8 = 64m

Cross Product also called Vector Product. Geometrically the Cross Product of 2 vectors is area of parallelogram between them.

A x B = C

A is the first, B is the second and C is the resultant. There is a right hand rule to determine the direction of the resultant. Just imagine that A is your finger, B is palm and C is your thumb.

Example :

If A is going to North and B is going to West. Just point your finger to North and face your palm to the West and see where is your thumb pointing at. Your thumb should be pointing Upwards.

I x I = J x J = K x K = (1) (1) (Sin 0) = 0

         I

K               J  

Now this is the IJK Triangle. If it turns in clockwise the result is positive but if it turns in anti-clockwise the result is negative.

Example ;

A = 4i + 3j - 2k

B = 7i + 2j + 5k

A x B = 8k - 21k - 13k - 14j - 20j - 34j + 15i + 4i + 19i = 38i - 68j - 26k

Measurements

Measuring is a process of the object in SI Unit.

Uncertainty

Uncertainty is the uncertain of the Measurement.

To find the Uncertainty in Vernier Caliper and Micrometer use this Formula :

▲X = ½ * Smallest Scale

Examples :

Vernier Caliper's Smallest Scale is 0.1 thus ▲X = ½ * 0.1 = 0.05 mm

Micrometer's Smallest Scale is 0.01 thus ▲X = ½ * 0.01 = 0.005 mm

Vernier Caliper

Look at the Picture. To read its Measurement first look at the Measurement of the First Scale. It stops at 10 cm. Then look at the Second Scale find the scale which is Aligned. Its 2 so its 0.2 cm.
Then sum it up 10.2 cm ± (Uncertainty) Which is 0.05 mm

Micrometer

Look at the Picture. To read its Measurement first look at the Measurement of the First Scale. It stops at 2.5 mm. Then look at the Second Scale fine the scale which is Aligned at the Picture. Its 12 so its 0.12 mm.

Then sum it up 2.62 mm ± (Uncertainty) Which is 0.005 mm

Another way to find Uncertainty is using this Formula :

1 ÷ N √((N(ΣI²) - (ΣI)²) ÷ (N - 1))

Example : (All in kg)

N                   I                   I²

1                   1                  1

2                   2                  4

3                   3                  9

4                   4                  16

5                   5                  25

1 ÷ 5 * √((5(55) - (15)²) ÷ (5 - 1)) = 1 ÷ 5 * √((275 - 225) ÷ 4) = 1 ÷ 5 * √(50 ÷ 4)

= 1 ÷ 5 * √12.5 ≈ 1 ÷ 5 * 3.54 ≈ 0.88 kg

Then find the Average of ΣI which is 15 ÷ 5 = 3 kg

Then the report of  the measurement is 3 kg ± 0.88 kg

To find the Accuracy use this Formula :

Uncertainty ÷ Average of ΣI * 100

Example :

0.88 ÷ 3 * 100 = 29%

Dimension

Dimension is an expression of the character of a derived quantity in relation to fundamental quantities, without regard for its numerical value.

Base Quantity                                         Dimension

Length                                                           L

Mass                                                             M

Time                                                              T

Current                                                          I

Temperature                                                 Θ (tetha)

Light Intensity                                               J

Number of Substance                                   N

Examples :

Normal Gravity is Meter / Second² so its [L] [T]^-2

Force is Mass * Meter / Second² so its [M] [L] [T]^-2

Work is Mass * Meter / Second² * Length so its [M] [L]² [T]^-2

Power is Mass * Meter / Second² * Length ÷ Second so its [M] [L]² [T]^-3

Sound Intensity is (Mass * Meter / Second² * Length ÷ Second) ÷ Meter² so its [M] [T]^-3